واریانس چیست؟ – به زبان ساده + مثال

امروزه داده‌های متفاوت، نقش مهمی را در علوم مختلف ایفا می‌کنند. این داده‌ها ممکن است حاوی اطلاعاتی در مورد سن، میزان تحصیلات، ضریب هوشی، نمره و بسیاری از اطلاعات دیگر در مورد افراد جوامع مختلف باشد. برای جمع‌آوری این داده‌ها باید از کل جمعیت جامعه یا قسمتی از جمعیت استفاده شود. پس از جمع‌آوری داده‌ها، پژوهش روی آن‌ها آغاز می‌شود. بر روی داده‌های آماری جمع‌آوری شده عملیات مختلفی را می‌توان انجام داد و کمیت‌های مختلفی را محاسبه کرد. واریانس یکی از این کمیت‌ها است که در این مطلب در مورد آن صحبت خواهیم کرد و تلاش می‌کنیم به پرسش واریانس چیست به زبانی ساده و گویا پاسخ دهیم.

با استفاده از واریانس می‌توانیم میزان پراکندگی داده‌ها را در مجموعه‌ای از داده‌ها اندازه بگیریم. همچنین، با استفاده از واریانس می‌توانیم فاصله هر متغیر از میانگین و متغیرهای دیگر را به‌دست آوریم. در بیشتر موارد واریانس با علامت $$sigma ^ 2$$ نشان داده می‌شود. معامله‌گران و تحلیل‌گران از این کمیت برای تعیین نوسانات و امنیت بازار استفاده می‌کنند. جذر واریانس، کمیت دیگری به نام انحراف معیار را به ما می‌دهد. در این مطلب از مجله فرادرس، ابتدا واریانس را تعریف می‌کنیم و با ذکر چند مثال ساده با مفهوم آن آشنا می‌شویم. سپس، در مورد انحراف معیار و تفاوت آن با واریانس صحبت می‌کنیم. در پایان، در مورد انواع واریانس و کاربردهای آن صحبت خواهیم کرد.

واریانس چیست؟

فرض کنید روبروی مدرسه ابتدایی ایستاده‌اید و از هر دانش‌آموزی که از مدرسه خارج می‌شود، سن او را می‌پرسید. از آنجا که این دانش‌آموزان در مدرسه ابتدایی درس می‌خوانند، محدوده سنی آن‌ها بین ۶ تا ۱۱ سال خواهد بود. در ادامه، همین کار را با دانشجویان یکی از دانشگاه‌های شهر خود انجام می‌دهید.

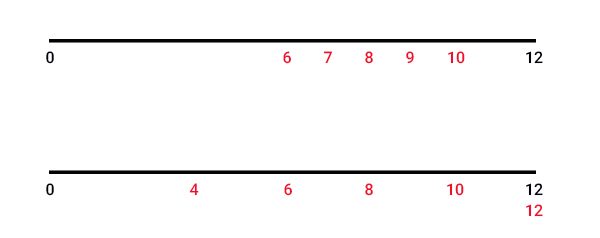
در حالت کلی، سن دانشجویان بین ۱۸ تا ۳۰ سال قرار می‌گیرد. اما گاهی استثناهایی نیز وجود دارند و ممکن است سن دانشجویی کمتر از ۱۸ یا بیشتر از ۳۰ سال باشد. به اطلاعات جمع‌آوری شده مربوط به سن دانش‌آموزان ابتدایی و دانشجویان در تصویر زیر دقت کنید. کمینه و بیشینه سن دانش‌آموزان ابتدایی به ترتیب برابر ۶ و ۱۱ سال و بازه سنی آن‌ها برابر ۵ سال است. اما کمینه و بیشینه سن دانشجویان در حالت کلی به ترتیب برابر ۱۸ و ۳۰ سال و بازه سنی آن‌ها برابر ۱۲ سال است.

به دو عدد ۵ و ۱۲ سال واریانس گفته می‌شود. واریانس به ما میزان پراکندگی داده‌های آماری جمع‌آوری شده را نشان می‌دهد. به بیان دیگر، واریانس اطلاعاتی را در مورد میزان تغییر مقدار داده‌های آماری بیان می‌کند. هرچه مقدار واریانس بزرگ‌تر باشد، میزان پراکندگی و تغییر داده‌های آماری نیز بیشتر خواهد بود. سوال مهمی که ممکن است مطرح شود آن است که آیا می‌توانیم عددی برای میزان تغییر و پراکندگی داده‌های آماری خود به‌دست آوریم یا خیر. پاسخ به این پرسش، بله است. با مثالی بسیار ساده نشان می‌دهیم که چگونه می‌توان مقدار عددی برای واریانس به‌دست آورد.

فرض کنید سه کودک با سن‌های چهار، پنج و شش سال داریم. برای به‌دست آوردن واریانس، ابتدا میانگین سنی این سه کودک را به‌دست می‌آوریم. برای محاسبه میانگین سنی سه کودک، سن آن‌ها را با یکدیگر جمع و عدد به‌دست آمده را بر تعداد، یعنی سه، تقسیم می‌کنیم.

$$Average = frac { 4 + 5 + 6 } { 3 } = 5 $$

بنابراین، میانگین سنی سه کودک برابر ۵ به‌دست می‌آید. در ادامه، سن هر کودک را به صورت جداگانه از میانگین سنی به‌دست آمده کم می‌کنیم. سن کودک اول برابر ۴ سال و تفاضل آن از میانگین سنی برابر است با:

$$4 – 5 $$

سن کودک دوم برابر ۵ سال و تفاضل آن از میانگین سنی برابر است با:

$$5 – 5 $$

سن کودک سوم نیز برابر ۶ سال و تفاضل آن از میانگین سنی برابر است با:

$$6 – 5 $$

در ادامه، هر یک از این تفاضل‌ها را به صورت جداگانه به توان دو می‌رسانیم و آن‌ها را با یکدیگر جمع می‌کنیم:

$$( 4 – 5 ) ^ 2 + ( 5 – 5 ) ^ 2 +  ( 6 – 5 )^ 2 $$

سپس،‌ از حاصل جمع به‌دست آمده میانگین می‌گیریم. از آنجا که سه کودک داریم، باید عبارت $$( 4 – 5 ) ^ 2 + ( 5 – 5 ) ^ 2 +  ( 6 – 5 )^ 2 $$ را بر سه تقسیم یا آن را در یک‌سوم ضرب کنیم.

$$frac { 1 } { 3 } times ( 4 – 5 ) ^ 2 + ( 5 – 5 ) ^ 2 +  ( 6 – 5 )^ 2 $$

حاصل عبارت فوق برابر $$frac { 2 } { 3 }$$ به‌دست می‌آید. در نتیجه، واریانس سن سه کودک برابر $$frac { 2 } { 3 }$$ است.

فرمول واریانس چیست؟

در بخش قبل فهمیدیم واریانس چیست و با مثالی بسیار ساده مقدار آن را به‌دست آوردیم. در این بخش با بیان فرمول ریاضی واریانس، مثال‌های پیچیده‌تری را با یکدیگر بررسی می‌کنیم. واریانس به صورت مربع حرف انگلیسی s یعنی $$s ^ 2$$ نشان داده می‌شود. شاید از خود بپرسید s به چه معنا است. s، انحراف معیار نام دارد. بنابراین، خالی از لطف نیست که قبل از بیان فرمول ریاضی واریانس، کمی در مورد انحراف معیار و چگونگی محاسبه آن صحبت کنیم.

انحراف معیار چیست؟

انحراف معیار به ما نشان می‌دهد که چگونه داده‌های آماری جمع‌آوری شده حول میانگین پراکنده شده‌اند. همین تعریف ساده به احتمال زیاد سوال مهمی را در ذهن شما ایجاد کرده است. به هنگام تعریف واریانس گفتیم که این کمیت اطلاعاتی در مورد میزان تغییر یا پراکندگی داده‌های آماری به ما می‌دهد. انحراف معیار و واریانس چه تفاوتی با یکدیگر دارند. در ادامه به این پرسش پاسخ خواهیم داد. انحراف معیار پراکندگی داده‌های آماری را به ما نشان می‌دهد. فرض کنید قد تعدادی از دوستان خود را اندازه گرفته‌اید. انحراف معیار به ما می‌گوید که مقدارهای به‌دست آمده برای قد افراد چگونه حول میانگین قدی آن‌ها پراکنده شده است.

ابتدا میانگین قدی را به‌دست می‌آوریم. برای محاسبه میانگین قدی، مقدارهای اندازه‌گیری شده برای قد هر یک از افراد را با یکدیگر جمع و حاصل را بر تعداد افراد تقسیم می‌کنیم. در حالت کلی، میانگی تعدادی داده عددی را با استفاده از فرمول زیر به‌دست می‌آوریم:

$$overline{ x } = frac { x_ 1 + x_ 2 + x_ 3 + . . . + x_ n } { n }$$

فرض کنید،‌ مقدار میانگین قد برابر ۱۵۵ سانتی‌متر به‌دست می‌آید. اکنون می‌خواهیم بدانیم قدِ هر فرد چه مقدار از میانگین به دست آمده فاصله دارد. به قدِ نخستین فرد توجه می‌کنیم. او ۱۸ سانتی‌متر از میانگین قدی به‌دست آمده بلندتر است. فرد دوم نیز ۸ سانتی‌متر از میانگین قدی کوتاه‌تر، فرد سوم ۱۵ سانتی‌متر کوتاه‌تر، فرد چهارم ۸ سانتی‌متر بلندتر، فرد پنجم ۹ سانتی‌متر کوتاه‌تر و فرد ششم ۶ سانتی‌متر بلندتر هستند. افرادی با قدِ بسیار کوتاه یا بسیار بلند فاصله یا انحراف بیشتری از میانگین قدی دارند. فاصله قد هر فرد از مقدار میانگین برای ما مهم نیست، بلکه میانگین انحراف قد افراد نسبت به مقدار میانگین برای ما مهم است. از این‌رو، با محاسبه انحراف معیار می‌توانیم مقدار میانگینِ انحراف قد افراد از مقدار میانگین را به‌دست آوریم. انحراف معیار در این مثال ساده برابر ۱۲/۰۶ سانتی‌متر است. انحراف معیار با استفاده از رابطه ریاضی زیر به‌دست می‌آید:

$$sigma = sqrt { frac { 1} { n } sum_{ i = 1 } ^ n (x_i – overline{ x } ) ^ 2 }$$

در رابطه فوق:

• $$sigma$$ انحراف معیار است.
• n تعداد افراد یا تعداد نمونه بررسی شده است.
• $$x_ i$$ مقدار هر نمونه است. به عنوان مثال، $$x_ i$$ در مثال اندازه‌گیری قد، قد هر فرد را نشان می‌دهد.
• $$overline { x }$$ مقدار میانگین را نشان می‌دهد.

در نتیجه، برای به‌دست آوردن انحراف میانگین، مرحله‌های زیر را طی می‌کنیم:

1. مقدار میانگین داده‌های آماری را به‌دست می‌آوریم.
2. تفاضل مقدار هر نمونه را از میانگین محاسبه و حاصل را به توان دو می‌رسانیم. این کار را برای تمام نمونه‌ها انجام می‌دهیم.
3. سپس، مربع تفاضل‌ها را با یکدیگر جمع و بر تعداد نمونه‌ها تقسیم می‌کنیم.
4. در پایان،‌ از حاصل کل، جذر می‌گیریم.

بنابراین، انحراف معیار را می‌توانیم به صورت متوسط جذرِ مجموعِ مربعِ تفاضل هر مقدار از مقدار میانگین، تعریف کنیم. توجه به این نکته مهم است که انحراف معیار را می‌توان با استفاده از دو فرمول به‌دست آورد. یکی از فرمول‌ها را کمی بالاتر نوشتیم:

$$sigma = sqrt { frac { 1} { n } sum_{ i = 1 } ^ n (x_i – overline{ x } ) ^ 2 }$$

فرمول دوم نیز به صورت زیر نوشته می‌شود:

$$s = sqrt { frac { 1} { n – 1 } sum_{ i = 1 } ^ n (x_i – overline{ x } ) ^ 2 }$$

تفاوت دو فرمول در چیست؟ در فرمول اول، مربع تفاضل از میانگین بر تعداد کل نمونه‌ها، n، اما در فرمول دوم، مربع تفاضل از میانگین بر تعداد کل نمونه‌ها منهای یک، n-1، تقسیم می‌شود. چرا؟ چرا دو رابطه برای محاسبه انحراف معیار وجود دارد؟ در حالت کلی، محاسبه انحراف معیار برای تعداد زیادی جمعیت یکی از محاسبات مهم در آمار است. به عنوان مثال، فرض کنید که می‌خواهید انحراف معیارِ قد تمام والیبالیست‌های ایرانی را به‌دست آورید. اگر قدِ تمام والیبالیست‌های ایرانی را بدانیم از رابطه $$sigma = sqrt { frac { 1} { n } sum_{ i = 1 } ^ n (x_i – overline{ x } ) ^ 2 }$$ برای محاسبه انحراف معیار استفاده می‌کنیم.

اما گاهی نمی‌توانید مطالعه آماری خود را روی تمام جمعیت موردنظر انجام دهید. بنابراین، تعدادی والیبالیست‌ را به عنوان نمونه آماری انتخاب کنید. از این جامعه آماری انتخاب شده برای تخمین انحراف معیار کل جمعیت والیبالیست‌های ایرانی و از رابطه $$s = sqrt { frac { 1} { n – 1 } sum_{ i = 1 } ^ n (x_i – overline{ x } ) ^ 2 }$$ برای محاسبه مقدار آن استفاده کنید.

تفاوت انحراف معیار و واریانس چیست؟

سوال مهم دیگری که ممکن است مطرح شود آن است که انحراف معیار چه تفاوتی با واریانس دارد:

• انحراف معیار مقدار فاصله اعداد را در مجموعه داده اندازه می‌گیرد. اما واریانس مقدار واقعی تفاوت اعداد از میانگین را در مجموعه داده می‌دهد.

• انحراف معیار، جذر واریانس و یکای آن مشابه یکای داده‌ها در مجموعه داده است. واریانس می‌تواند به صورت مجذور یا درصد بیان شود (در داده‌های مالی این مورد مطرح می‌شود).
• انحراف معیار می‌تواند از واریانس بزرگ‌تر باشد، زیرا جذر اعداد اعشاری کوچک‌تر از یک از عدد اصلی بزرگ‌تر خواهد بود. به عنوان مثال، جذر ۰/۱ در حدود ۰/۳ است.
• اگر واریانس از یک بزرگ‌تر باشد، انحراف معیار کوچک‌تر خواهد بود.

تفاوت این دو کمیت به صورت خلاصه در جدول زیر نوشته شده‌اند.

	انحراف معیار	واریانس
چیست؟	جذر واریانس	متوسطِ مربعِ تفاضلِ هر مقدار از میانگین
چه چیزی را نشان می‌دهد؟	پراکندگی بین اعداد در مجموعه داده	میانگین تفاوت هر نقطه با میانگین داده‌ها
چگونه بیان می‌شود؟	با یکای مشابه داده‌ها	یکاهای مربع یا درصد
چه معنایی دارد؟	انحراف معیار کوچک (پراکندگی کوچک) به معنای نوسان کم و انحراف معیار بزرگ (پراکندگی بزرگ) به معنای نوسان بیشتر است.	تغییر میزان بازده برحسب زمان

تا اینجا می‌دانیم انحراف معیار و واریانس چیست و چه تفاوت‌هایی با یکدیگر دارند. همچنین، با چگونگی محاسبه انحراف معیار آشنا شدیم. در تفاوت واریانس و انحراف معیار به این نکته اشاره کردیم که انحراف معیار از جذر واریانس به‌دست می‌آید. در نتیجه، واریانس با استفاده از فرمول زیر محاسبه می‌شود:

$$ frac { 1} { n } sum_{ i = 1 } ^ n (x_i – overline{ x } ) ^ 2 $$

از این‌رو، واریانس مربع انحراف معیار و انحراف معیار، جذر واریانس است. از آنجا که واحد واریانس با داده‌های مجموعه داده یکسان نیست، در بیشتر موارد از انحراف معیار برای توصیف نمونه‌ها استفاده می‌شود.

محاسبه واریانس

همان‌طور که در مطالب بالا اشاره شد، واریانس با $$s ^ 2$$ نشان داده می‌شود. با حل چند مثال ساده، واریانس مجموعه داده‌های مختلف را با یکدیگر محاسبه می‌کنیم.

مثال اول محاسبه واریانس

واریانس داده‌های زیر را حساب کنید.

$$6, 9, 14, 10, 5 , 8, 11$$

پاسخ

برای محاسبه واریانس، مراحل زیر را طی می‌کنیم:

1. مقدار میانگین داده‌های آماری را به‌دست می‌آوریم.
2. تفاضل مقدار هر نمونه را از میانگین محاسبه و حاصل را به توان دو می‌رسانیم. این کار را برای تمام نمونه‌ها انجام می‌دهیم.
3. سپس، مربع تفاضل‌ها را با یکدیگر جمع و بر تعداد نمونه‌ها تقسیم می‌کنیم.

بنابراین، در مرحله اول میانگین اعداد داده شده را به‌دست می‌آوریم:

$$overline{ x } = frac { x_ 1 + x_ 2+ … + x_ 7 } { 7 } overline { x } = frac { 6 + 9 + 14 + 10 + 5 + 8 + 11 } { 7 } = frac { 63 } { 7 } = 9$$

در مرحله دوم،‌ تفاضل مقدار هر نمونه را از میانگین محاسبه و حاصل را به توان دو می‌رسانیم. این کار را برای هر هفت عدد داده شده انجام می‌دهیم. این محاسبات در جدول زیر نوشته شده است.

عدد داده شده	مقدار میانگین	تفاضل عدد و مقدار میانگین	مربع تفاضل
6	9	$$6 – 9$$	$$(6-9)^ 2$$
9	9	$$9-9$$	$$(9 – 9 ) ^ 2$$
14	9	$$14-9$$	$$(14 – 9 ) ^ 2$$
10	9	$$10-9$$	$$(10 – 9 ) ^ 2$$
5	9	$$5-9$$	$$( 5 – 9 ) ^ 2$$
8	9	$$8-9$$	$$( 8 – 9 ) ^ 2$$
11	9	$$11-9$$	$$(11- 9 ) ^ 2$$

در ادامه، مربع تفاضل نوشته شده در ستون آخر را با یکدیگر جمع می‌کنیم:

$$(6 – 9 ) ^ 2 + ( 9 – 9 ) ^ 2 + ( 14 – 9 ) ^ 2 + ( 10 – 9 ) ^ 2 + ( 5- 9 ) ^ 2 + ( 8 – 9 ) ^ 2 + ( 11 – 9 ) ^ 2 = ( – 3 ) ^ 2 + 0 + 5 ^ 2 + 1 + ( – 4 ) ^ 2 + ( -1 ) ^ 2 + 2 ^ 2 = 9 + 25 + 1 + 16 + 1 + 4 = 56 $$

در مرحله آخر، عدد به‌دست آمده را بر تعداد نمونه‌ها یعنی هفت تقسیم می‌کنیم:

$$frac { 56 } { 7 } = 8$$

به این نکته توجه داشته باشید که اگر اعداد داده شده بخشی از مجموعه داده بزرگ‌تری باشند، عدد ۵۶ را بر ۶ ($$n -1$$) تقسیم می‌کردیم. اما برای این مثال فرض می‌کنیم که اعداد داده شده همان مجموعه داده مورد مطالعه است.

مثال دوم محاسبه واریانس

فرض کنید دو مجموعه داده یک و دو با اعداد زیر داریم:

$$data enspace set enspace 1 : 6 , 7, 8, 9, 10 data enspace set enspace 2 : 4, 6 , 8 , 10 . 12$$

واریانس کدام مجموعه داده بزرگ‌تر است؟

پاسخ

برای پاسخ به این مثال، واریانس هر مجموعه داده را به صورت جداگانه به‌دست می‌آوریم.

محاسبه واریانس مجموعه داده یک

جدولی را مشابه جدول مثال اول تهیه می‌کنیم:

عدد داده شده	مقدار میانگین	تفاضل عدد و مقدار میانگین	مربع تفاضل
6	8	$$6 – 8$$	$$(6-8)^ 2$$
7	8	$$7-8$$	$$(7-8 ) ^ 2$$
8	8	$$8-8$$	$$(8-8 ) ^ 2$$
9	8	$$9-8$$	$$(8 – 9 ) ^ 2$$
10	8	$$10-8$$	$$( 10-8 ) ^ 2$$

در ادامه، مربع تفاضل نوشته شده در ستون آخر را با یکدیگر جمع می‌کنیم:

$$(6 – 8 ) ^ 2 + ( 7-8 ) ^ 2 + ( 8-8 ) ^ 2 + ( 9 – 8 ) ^ 2 + ( 10 – 8 ) ^ 2 = ( – 2 ) ^ 2 + 1 + 0 + 1 + 2 ^ 2 = 4+1+1+4 = 10 $$

در مرحله آخر، عدد به‌دست آمده را بر تعداد نمونه‌ها یعنی پنج تقسیم می‌کنیم:

$$frac { 10 } { 5 } = 2$$

محاسبه واریانس مجموعه داده یک

جدولی را مشابه جدول مثال اول تهیه می‌کنیم:

عدد داده شده	مقدار میانگین	تفاضل عدد و مقدار میانگین	مربع تفاضل
4	8	$$4 – 8$$	$$(4-8)^ 2$$
6	8	$$6-8$$	$$(6-8 ) ^ 2$$
8	8	$$8-8$$	$$(8-8 ) ^ 2$$
10	8	$$10-8$$	$$(8 – 10 ) ^ 2$$
12	8	$$12-8$$	$$( 12-8 ) ^ 2$$

در ادامه، مربع تفاضل نوشته شده در ستون آخر را با یکدیگر جمع می‌کنیم:

$$(4 – 8 ) ^ 2 + ( 6-8 ) ^ 2 + ( 8-8 ) ^ 2 + ( 10 – 8 ) ^ 2 + ( 12 – 8 ) ^ 2 = 4 ^ 2 + 2^ 2 + 0 + 2 ^ 2 + 4 ^ 2 = 16+4 + 0+ 4 + 16 = 40 $$

در مرحله آخر، عدد به‌دست آمده را بر تعداد نمونه‌ها یعنی پنج تقسیم می‌کنیم:

$$frac { 40 } { 5 } = 8$$

همان‌طور که مشاهده می‌شود واریانس مجموعه داده‌های دوم از واریانس مجموع داده‌های اول بزرگ‌تر است. داده‌های مجموعه داده یک و دو را به صورت نشان داده شده در تصویر زیر روی محور افقی رسم می‌کنیم. میانگین مجموعه داده یک و دو برابر ۸ به‌دست آمد. این عدد با یکی از داده‌های هر یک از مجموعه‌ها برابر است. همان‌طور که در تصویر زیر دیده می‌شود، پراکندگی داده‌ها در مجموعه دو بیشتر از مجموعه یک است. از آنجا که پراکندگی داده‌ها در مجموعه داده دوم بیشتر از مجموعه داده اول است، انتظار داریم واریانس آن نیز بزرگ‌تر از مجموعه داده اول باشد. انتظاری که بر طبق محاسبات انجام شده، برآورده شد.

مثال سوم محاسبه واریانس

تعداد رونویسی‌های mRNA از ژن X در ۵ سلول متفاوت کبد شمارش شده‌اند. به تصویر زیر توجه کنید. دایره سبز‌رنگ نشان داده شده در این تصویر سلول کبدی با ۳ رونویسی mRNA برای ژن X را نشان می‌دهد.

دایره سبزرنگ دوم در تصویر زیر نیز سلول کبدی با ۱۳ رونویسی mRNA را نشان می‌دهد.

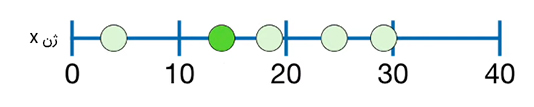
همچنین، سه دایره باقی‌مانده سبز‌رنگ نیز به ترتیب ۱۹، ۲۴ و ۲۹ رونویسی mRNA را نشان می‌دهند. در صورت داشتن زمان و پولِ کافی می‌توانستیم تعداد رونویسی‌های mRNA را برای ژن X در تمام ۲۴۰ میلیارد سلول‌های کبد بشماریم. در ادامه، نمودار هیستوگرام اندازه‌گیری‌های انجام شده را رسم می‌کنیم.

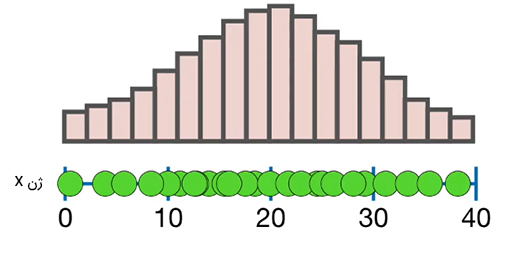
اگر بخواهیم نمودار مناسبی را روی نمودار هیستوگرام بیندازیم، باید «میانگین جمعیت» (Population Mean)، «واریانس جمعیت» (Population Variance) یا «انحراف معیار جمعیت» (Standard Deviation Population) را محاسبه کنیم. محاسبه میانگین جمعیت راحت است. برای انجام این کار، تنها کافی است میانگین تمام ۲۴۰ میلیارد اندازه‌گیری‌های انجام شده را به‌دست آوریم.

$$Population mean = frac { 1 + 3 + 5 + … + 26 + 37 } { 240000000000} = 20$$

سپس، میانگین جمعت به‌دست آمده را در مرکز نمودار برازش شده به صورت نشان داده شده در تصویر زیر قرار می‌دهیم. به این نکته توجه داشته باشید که در اینجا میانگین را با استفاده از ۲۴۰ میلیارد اندازه‌گیری انجام شده به‌دست آوردیم. بنابراین، عدد به‌دست آمده تخمینی برای میانگین جمعیت نیست، بلکه مقدار دقیق میانگین را به ما می‌دهد. اما از آنجا که در بیشتر مواقع زمان و پول کافی برای اندازه‌گیری تمام نمونه‌های آماری موجود در جامعه آماری را نداریم، با استفاده از تعدادی نمونه انتخاب شده، میانگین جمعیت را به صورت تخمینی محاسبه می‌کنیم. در این مثال، تنها ۵ نمونه از تعداد ۲۴۰ میلیارد نمونه اندازه‌گیری شده‌اند.

در این حالت، محاسبه میانگین جمعیت به صورت تخمینی بسیار ساده است. تنها کافی است میانگین ۵ نمونه اندازه‌گیری شده را به‌دست آوریم.

$$Estimated enspace mean = frac { 3 + 13 +19+ 24 + 29 } { 5 } = 17.6$$

به این نکته توجه داشته باشید که در جامعه آماری از $$overline { x }$$ f برای میانگین تخمینی و از نماد $$mu$$ برای اشاره به میانگین جمعیت استفاده می‌شود. $$overline { x }$$ f و $$mu$$ با یکدیگر تفاوت دارند. اما هر اندازه تعداد داده‌های اندازه‌گیری شده بیشتر باشند، $$overline { x }$$ f و $$mu$$ به یکدیگر نزدیک‌تر می‌شوند. در ادامه، با محاسبه واریانس و انحراف معیار می‌خواهیم مقدار عرض نمودار برازش شده را به‌دست آوریم. به بیان دیگر، می‌خواهیم مقدار پراکندگی داده‌ها حول میانگین جمعیت را به‌دست آوریم. همان‌طور که در بخش‌های قبل اشاره کردیم، برای محاسبه واریانس جمعیت از رابطه زیر استفاده می‌کنیم:

$$Population enspace Variance = frac { sum ( x – mu ) ^2 }
{ n }$$

توجه به این نکته مهم است که با استفاده از این فرمول واریانس جمعیت را به طور دقیق می‌توانیم به‌دست آوریم. در رابطه فوق، $$x$$ مقدار اندازه‌گیری شده برای هر داده است. با انجام محاسبات لازم، مقدار واریانس جمعیت، برابر ۱۰۰ به‌دست می‌آید. با محاسبه واریانس به خود افتخار می‌کنیم، اما مسئله‌ای آزاردهنده وجود دارد. از آنجا که تفاضل مقدار هر نمونه از میانگین به توان دو رسیده است، یکای عدد به‌دست آمده، ۱۰۰، برابر رونویسی mRNA به توان دو خواهد بود. به همین دلیل نمی‌توانیم واریانس را روی نمودار نشان دهیم.

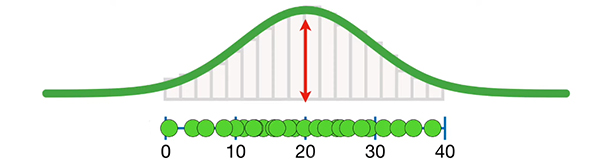
برای حل این مشکل می‌توانیم، از واریانس جذر بگیریم و کمیتی به نام انحراف معیار را به‌دست آوریم. از این‌رو، مقدار انحراف معیار جمعیت برابر $$sqrt { 100 } = 10$$ است. این عدد را می‌توانیم روی نمودار رسم کنیم. نمودار رسم شده در تصویر زیر، مقدار میانگین، ۲۰، را همراه با به اضافه و منهای انحراف معیار، ۱۰ رونویس mRNA، نشان می‌دهد.

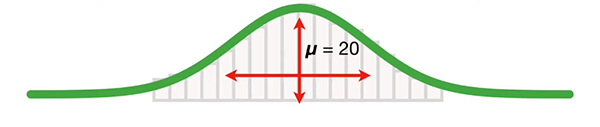
قبل از ادامه این مثال به این نکته توجه داشته باشید که ما هرگز داده‌های مربوط به تمام نمونه‌های داخل جامعه آماری را نداریم. بنابراین، میانگین، واریانس و انحراف معیار جمعیت مورد مطالعه را نمی‌توانیم به طور دقیق محاسبه کنیم. به جای محاسبه دقیق این کمیت‌ها، با انتخاب جامعه آماری کوچک‌تری از جامعه آماری بزرگ‌تر، مقدار آن‌ها را تخمین می‌زنیم. برای تخمین واریانس از رابطه زیر استفاده می‌کنیم:

$$Estimated enspace Population enspace Variance
= frac { sum ( x – overline { x } ) ^2 } { n – 1 }$$

از آنجا که بیشتر مواقع با مجموعه کوچکی از جمعیت و نه کل جمعیت سروکار داریم، استفاده از این فرمول برای محاسبه واریانس رایج‌تر است. در این فرمول به جای تقسیم بر n، بر n-1 تقسیم می‌کنیم. همچنین، هر داده را از میانگین مجموعه انتخاب شده و نه از میانگین کل جمعیت کم می‌کنیم. مجموعه انتخاب شده از جمعیت کل از ۵ داده با میانگین ۱۷/۶ تشکیل شده است. واریانس این مجموعه به صورت زیر و به صورت تخمینی محاسبه می‌شود:

$$Estimated enspace Population enspace Variance
= frac { sum ( x – overline { x } ) ^2 } { n – 1 } frac
{ ( 3 -17.6 ) ^ 2 + (13 – 17.6 ) ^ 2 + ( 19 – 17.6 ) ^ 2 + ( 29 –
17.6 ) ^ 2 } { 5 – 1 } $$

مقدار واریانس به صورت تقریبی برابر ۱۰۱/۸ به‌دست می‌آید. برای به‌دست آوردن مقدار تقریبی انحراف معیار، تنها کافی است که از این مقدار جذر بگیریم. در نتیجه، مقدار انحراف معیار نیز به صورت تقریبی برابر ۱۰/۱ به‌دست می‌آید. پارامترهای جمعیت تقریبی به شکل نمودار بنفشِ نشان داده شده در تصویر زیر با مقدار میانگین ۱۷/۶ و انحراف معیار ۱۰/۱ است.

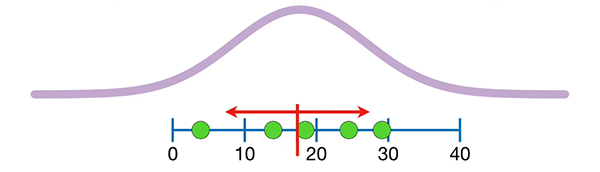
این نمودار تفاوت زیادی با نمودار رسم شده با مقدار میانگین و انحراف معیار دقیق ندارد.

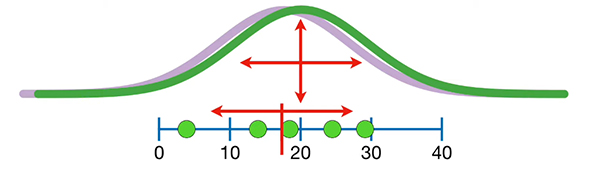
هر چه تعداد داده‌های انتخاب شده از مجموعه آماری کل بیشتر باشد، کمیت‌های تقریبی به مقدار واقعی نزدیک‌تر خواهند بود. گرچه با انتخاب ۵ داده هم هنوز به مقدار واقعی نزدیک هستیم.

محاسبه واریانس در اکسل

برای محاسبه واریانس در اکسل ابتدا باید داده‌های خود را در اکسل وارد کنیم. پس از وارد کردن داده‌ها در اکسل می‌توانیم با توجه به نوع داده‌ها و نوع واریانسی که می‌خواهیم، فرمول موردنظر را در اکسل انتخاب کنیم. همان‌طور که می‌دانیم برای محاسبه واریانس گاهی از تمام داده‌ها استفاده می‌کنیم و گاهی مجموعه کوچکی از داده‌ها را انتخاب و واریانس را به‌دست می‌آوریم. با استفاده از اکسل به راحتی می‌توانیم هر دو کار را انجام دهیم. محاسبه واریانس توسط اکسل به اندازه داده‌ها مربوط می‌شود.

اگر مجموعه داده کوچک باشد از توابع VAR

  و VAR.S

  یا VARA

  استفاده می‌کنیم. همچنین، برای محاسبه واریانس جمعیت باید از فرمول‌های VARP

  و VAR.P

  یا VARPA

  استفاده کنیم. بنابراین، در اکسل می‌توانیم دو نوع واریانس را به‌دست آوریم:

1. واریانس جمعیت: در این حالت، واریانس تمام داده‌ها را با استفاده از VARP

     و VAR.P

     یا VARPA

     به‌دست می‌آوریم.

2. واریانس نمونه: در این حالت، واریانس قسمتی از داده‌ها را با استفاده از VAR

     و VAR.S

     یا VARA

     به‌دست می‌آوریم.

از میان شش تابع فوق، دو تابع VAR

  و VARP

  منسوخ و به ترتیب با دو تابع VAR.S

  و VAR.P

  جایگزین شده‌اند. توابع VAR

  و VAR.S

  تنها با متغیرهای عددی کار می‌کنند. اما اگر بخواهیم از رشته‌های متنی یا منطقی استفاده کنیم، تابع VARA

  به کمک ما می‌آید. همچنین، برای محاسبه واریانس جمعیتِ رشته‌های متنی یا منطقی باید از تابع VARPA

  استفاده کنیم. از واریانس برای تعیین میزان پراکندگی داده‌ها حول میانگین استفاده می‌شود. در این حالت، رشته‌های متنی و نتایج منطقی به معادل‌های عددی تبدیل می‌شوند. برای این تبدیل، رشته متنی به صورت صفر یا FALSE محاسبه خواهد شد. این کار می‌تواند بر نتایج کلی تاثیر داشته باشد. از این‌رو، توابع باید با دقت انتخاب شوند.

این توابع در اکسل به صورت زیر استفاده می‌شوند:

فرمول اول:

= VAR  ( value 1 , value 2 , ...)

فرمول دوم:

= VAR.S  ( value 1 , value 2 , ...)

فرمول سوم:

VARP  ( value 1 , value 2 , ...)

فرمول چهارم:

VAR.P  ( value 1 , value 2 , ...)

فرمول پنجم:

VARA  ( value 1 , value 2 , ...)

فرمول ششم:

VARPA  ( value 1 , value 2 , ...)

برای محاسبه واریانس در اکسل باید مرحله‌های زیر را طی کنیم. اگر مجموعه‌ای مشتکل از چند داده را از مجموعه‌ای بزرگ‌تر انتخاب کرده باشیم باید از توابع VAR

  و VAR.S

  یا VARA

  استفاده کنیم. در صورتی که بخواهیم واریانس تمام داده‌ها را به‌دست آوریم از توابع VARP

  و VAR.P

  یا VARPA

  استفاده می‌کنیم. به این نکته توجه داشته باشید که دو تابع VAR

  و VAR.S

  قابل تعویض هستند. اما تابع VAR.S جدیدتر است. حالت مشابهی نیز برای دو تابع VARP

  و VAR.P

  وجود دارد. تابع VAR.P

  در نسخه‌های جدیدتر اکسل استفاده می‌شود.

مرحله اول

فایل اکسل حاوی داده‌های خود را باز و سلولی خالی انتخاب می‌کنیم. سپس روی نوار فرمول به صورت نشان داده شده در تصویر زیر کلیک می‌کنیم.

مرحله دوم

در این مرحله، داخل نوار فرمول عبارت =VAR.S ()

  یا ‌ = VARA ()

  را می‌نویسیم. اگر بخواهیم از کل داده‌ها استفاده کنیم، باید داخل نوار فرمول عبارت = VAR. P ()

  یا = VARPA ()

  را بنویسیم.

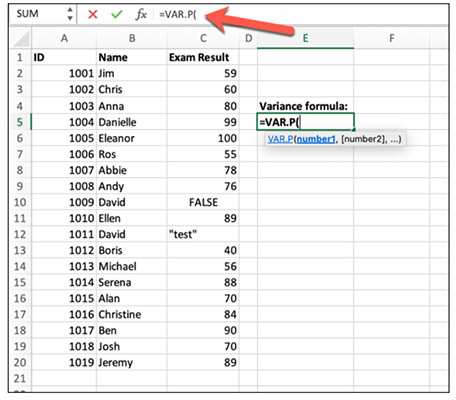
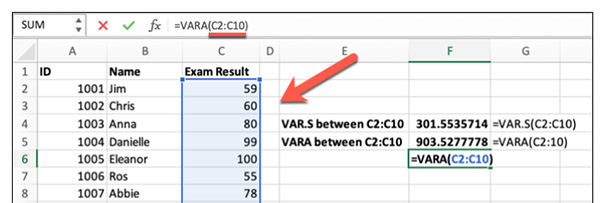
در ادامه، باید داده‌ها را در فرمول قرار دهیم. برای قرار دادن داده‌ها در فرمول واریانس یا باید داده‌ها را انتخاب یا آدرس آن‌ها را داخل فرمول بنویسیم. به عنوان مثال، در تصویر نشان داده شده در بالا، نمره‌های دانش‌آموزان در ستون C از ردیف ۲ تا ۲۰ قرار گرفته‌اند. در اینجا می‌توانیم:

• از فرمول VAR.S

    استفاده کنیم و داده‌های قرار گرفته از سلول C2 تا C10 را در آن قرار دهیم ( = VAR.S ( C2:C10)

   ).

• از فرمول VAR.P

    استفاده کنیم و داده‌های قرار گرفته از سلول C2 تا C20 را در آن قرار دهیم ( = VAR.S ( C2:C20)

   ).

کوواریانس چیست؟

تا اینجا می‌دانیم واریانس چیست و چگونه محاسبه می‌شود. در این بخش در مورد کوواریانس صحبت می‌کنیم. در مثال سوم از بخش قبل در مورد مجموعه‌ای از ۵ رونویس mRNA در ژن X از ۵ سلول متفاوت و داده‌های آماری آن‌ها صحبت کردیم. اکنون فرض کنید علاوه بر شمارش رونویس‌های mRNA برای ژن X، رونویس‌های ژن Y در ۵ سلول مشابه را نیز می‌شماریم.

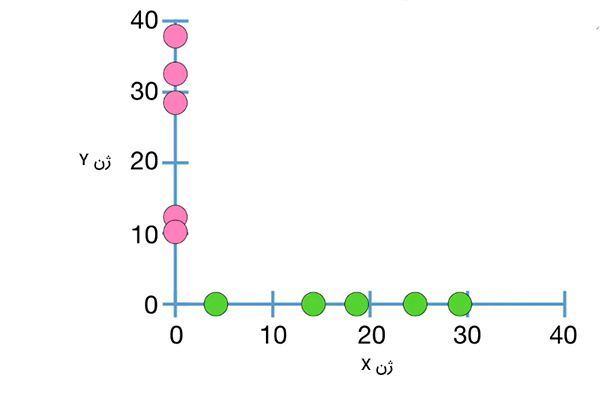
همان‌طور که در تصویر فوق مشاهده می‌کنید نمودار ژن Y بر نمودار ژن X عمود است. چرا؟ در ادامه علت این موضوع را خواهید فهمید. میانگین داده‌های ژن Y برابر ۲۴/۴ است و میانگین آن‌ها را با $$overline { y }$$ نشان می‌دهیم. با داشتن میانگین داده‌ها، به راحتی می‌توانیم واریانس را به‌دست آوریم. این مقدار برابر ۱۶۰/۳ است. در مثال ۳ از بخش قبل و در این قسمت میانگین و واریانس دو ژن متفاوت در پنج سلول مشابه را به صورت تقریبی محاسبه کرده‌ایم. از آنجا که این اندازه‌گیری‌ها در سلول‌های مشابهی انجام شده است، آن‌ها را می‌توانیم به صورت جفتی بررسی کنیم.

از آنجا که این دو اندازه‌گیری را می‌توان به صورت جفت و با یکدیگر بررسی کرد، سوال مهمی که ممکن است مطرح شود آن است که آیا اندازه‌گیری‌های جفتی اطلاعات بیشتری در مقایسه با اندازه‌گیری‌های تکی به ما می‌دهند یا خیر؟ با استفاده از مفهومی به نام کوواریانس می‌توانیم به این پرسش پاسخ دهیم. از آنجا که اندازه‌گیری‌ها در سلول‌های مشابهی انجام شده‌اند، می‌توانیم هر جفت را به صورت نقطه‌ای تک و با ترکیب کردن مقدارهای x و y رسم کنیم. با توجه به نمودار نشان داده شده در تصویر زیر مشاهده می‌کنیم که سلول‌هایی با مقدارهای کوچک برای ژن X، مقدارهای کوچکی نیز برای ژن Y دارند.

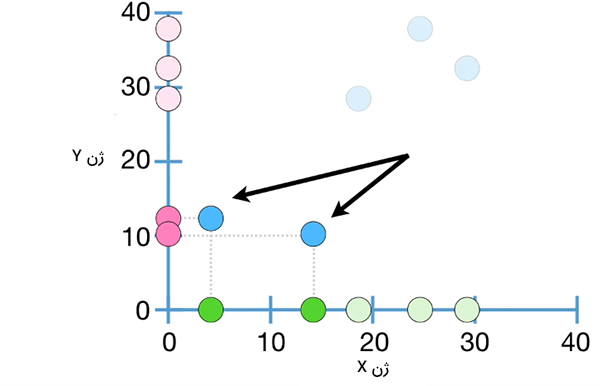
به طور مشابه، سلول‌هایی با مقدارهای بزرگ برای ژن X، مقدارهای نسبتا بزرگی نیز برای ژن Y دارند. این رابطه، اندازه‌گیری‌های کوچک برای دو ژن در برخی سلول‌ها و اندازه‌گیری‌های بزرگ برای دو ژن در سلول‌های دیگر را می‌توان به صورت خلاصه با خط رسم شده در تصویر زیر خلاصه کرد. شیب خطی که این ویژگی خاص را نشان می‌دهد، مثبت خواهد بود. با دنبال کردن این خط می‌بینیم که مقدارهای ژن X و ژن Y با یکدیگر افزایش می‌یابند. به بیان دیگر، اگر به شما گفته شود که رونویس‌های بسیاری برای ژن X در سلولی وجود دارند،‌ روند مشاهده شده از روی خط رسم شده پیشنهاد می‌کند که سلول مشابه باید تعداد زیادی رونویس برای ژن Y داشته باشد. به طور مشابه اگر مقدار‌ ژن Y کوچک باشد، روند مشاهده شده برحسب خط رسم شده پیشنهاد می‌کند که سلول مشابه، تعداد کمی رونویس برای ژن X دارد.

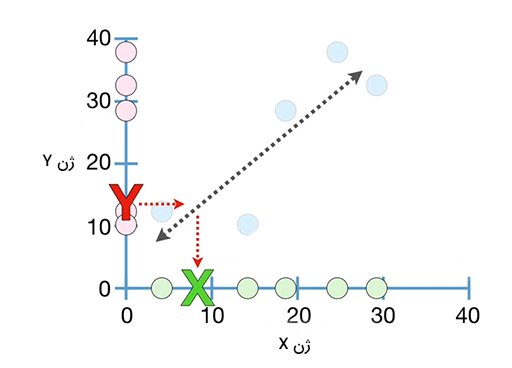
اکنون فرض کنید داده‌های به‌دست آمده به شکل نشان داده شده در تصویر زیر هستند. در این حالت، مقدار‌های نسبتا کم برای ژن X متناظر با مقدارهای نسبتا زیاد برای ژن Y و مقدار‌های نسبتا زیاد برای ژن X متناظر با مقدارهای نسبتا کم برای ژن Y هستند. در این حالت، خط رسم شده برای داده‌های اندازه‌گیری شده شیب منفی خواهد داشت. روند مشاهده شده در این حالت نشان می‌دهد که مقدارهای ژن X با کاهش مقدار‌های ژن Y، افزایش می‌یابد.

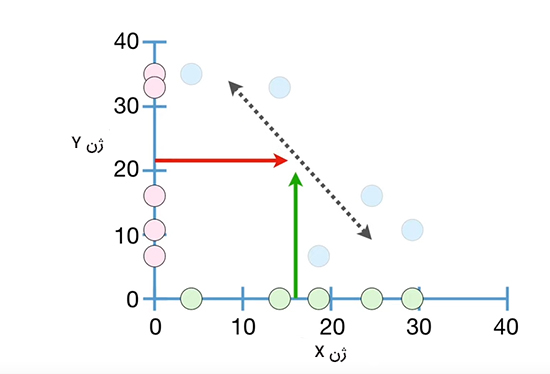
داده‌های اندازه‌گیری شده ممکن است به صورت نشان داده شده در تصویر زیر باشند. در این حالت هر مقدار برای ژن X با همان مقدار برای ژن Y جفت شده است. در این حالت، هیچ روندی، چه مثبت و چه منفی، مشاهده نمی‌شود.

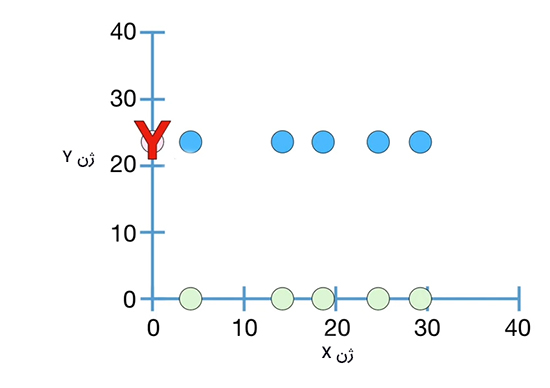
به طور مشابه، داده‌های اندازه‌گیری شده ممکن است به صورت نشان داده شده در تصویر زیر باشند. در این حالت هر مقدار برای ژن Y با همان مقدار برای ژن X جفت شده است. در این حالت نیز هیچ روندی، چه مثبت و چه منفی، مشاهده نمی‌شود.

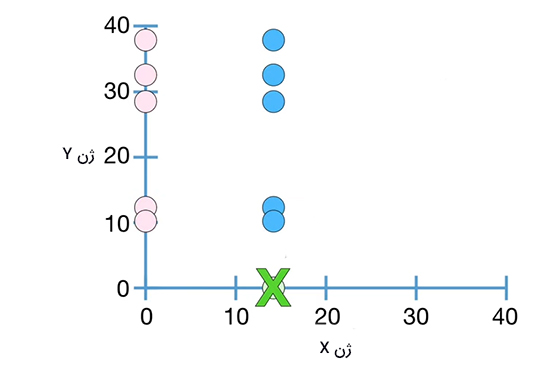
ایده اصلی پنهان شده در کوواریانس آن است که این کمیت سه نوع رابطه را به ما می‌دهد:

• رابطه‌ای با روند مثبت
• رابطه‌ای با روند منفی
• رابطه‌ و هیچ روندی وجود ندارد.

محاسبه کوواریانس

تاکنون با ایده اصلی پنهان شده در کوواریانس آشنا شده‌ایم. ایده دیگری نیز در کوواریانس وجود دارد، اما کمی آزاردهنده است. کوواریانس به تنهایی کمیت جالبی نیست. این بدان معنا است که هیچ‌گاه با محاسبه این کمیت، روز خود را به راحتی به اتمام نمی‌رسانید. بلکه، کوواریانس پله‌ای محاسباتی برای کمیت جالب دیگری، مانند همبستگی، است. همچنین، برای مشخص کردن رابطه بین دو متغیر تصادفی، در اینجا داده‌های ژن X و Y، از کوواریانس استفاده می‌کنند. این کمیت با استفاده از فرمول زیر محاسبه می‌شود:

$$frac { sum ( x – overline { x } ) ( y – overline { y } ) } { n – 1 }$$

در نتیجه، برای محاسبه کوواریانس، ابتدا باید میانگین داده‌های ژن‌های X و Y را محاسبه کنیم. مقدار متوسط داده‌های ژن X را به‌دست می‌آوریم و آن را روی نمودار افقی نشان می‌دهیم. سپس، خطی را موازی محور y از $$overline { x }$$ به صورت نشان داده شده در تصویر زیر رسم می‌کنیم.

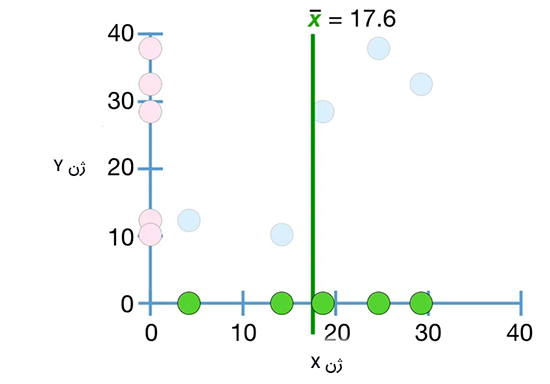
در ادامه، مقدار متوسط داده‌های ژن Y را به‌دست می‌آوریم و آن را روی نمودار عمودی نشان می‌دهیم. سپس، خطی را موازی محور x از $$overline { y }$$ به صورت نشان داده شده در تصویر زیر رسم می‌کنیم.

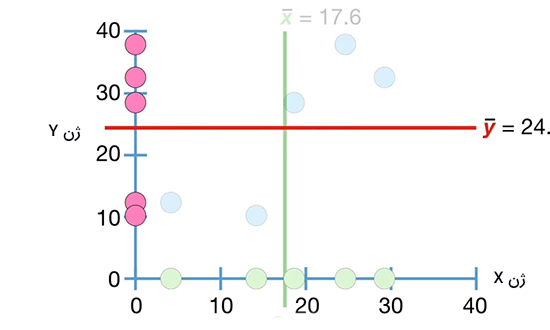
در ادامه، داده‌های سمت چپ و پایین نمودار را در نظر می‌گیریم. از آنجا که این داده‌ها در سمت چپ خط سبزرنگ ($$overline { x }$$) قرار گرفته‌اند، مقدار آن‌ها کمتر از $$overline { x }$$ است. همچنین، این داده‌ها پایین خط قرمزرنگ ($$overline { y }$$) قرار گرفته‌اند. بنابراین، مقدار آن‌ها کمتر از $$overline { y }$$ خواهد بود.

سپس، اندازه‌گیری انجام شده برای این داده‌ها را در رابطه $$frac { sum ( x – overline { x } ) ( y – overline { y } ) } { n – 1 }$$ قرار می‌دهیم. از آنجا که مقدار آن‌ها از $$overline { x }$$ و $$overline { y }$$ کمتر است، حاصل عبارت‌های $$x – overline { x }$$ و $$y – overline { y }$$ منفی به‌دست می‌آیند. سپس، مقدارهای به‌دست آمده برای هر تفاضل را در یکدیگر ضرب می‌کنیم. حاصل به‌دست آمده برای اولین داده اندازه‌گیری به صورت زیر نوشته می‌شود:

$$(3 – 17.6 ) times ( 12 – 24.4 ) = ( -14.6 ) times ( – 12.4 ) = 181$$

در ادامه، کار مشابهی را برای دومین داده انجام می‌دهیم:

$$(13 – 17.6 ) times ( 10 – 24. 4 ) = ( -4.6) times ( -14.4 ) = 66.2 $$

این دو داده در تصویر زیر نشان داده شده‌اند.

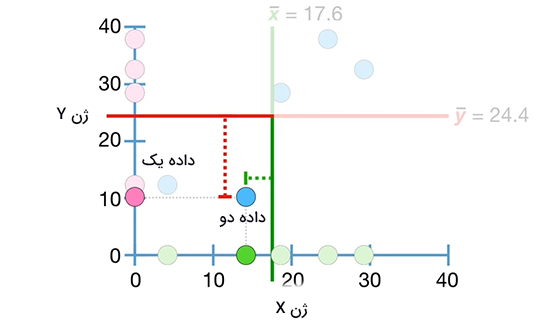
سه داده باقی‌مانده، سمت راست نمودار قرار گرفته‌اند. این سه داده بالای خط قرمزرنگ ($$overline { y }$$) و سمت راست خط سبزرنگ ($$overline { x }$$) قرار گرفته‌اند. بنابراین، مقدار آن‌ها بیشتر از $$overline { y }$$ و $$overline { x }$$ خواهد بود. مقدار این داده‌ها را نیز در رابطه $$frac { sum ( x – overline { x } ) ( y – overline { y } ) } { n – 1 }$$قرار می‌دهیم.

$$( 19 – 17.6 ) times ( 29 – 24. 4 ) + ( 24 – 17. 6 ) times ( 33 – 24. 4 ) + (  29 – 17. 6 ) times ( 38 – 24 . 4 ) = 6.4 + 55 + 155 = 216.4$$

عدد ۲۱۶/۴ را با عددهای ۱۸۱ و ۶۶/۲ جمع و حاصل به‌دست آمده را بر تعداد اندازه‌گیری‌های، ۵، منهای یک تقسیم می‌کنیم:

$$frac { 181+ 66.2 + 216.4 } { 4 } = 116$$

در نتیجه، مقدار کوواریانس برابر ۱۱۶ به‌دست می‌آید. از آنجا که مقدار کوواریانس مثبت است، شیب بین ژن X و ژن Y نیز مثبت خواهد بود. به بیان دیگر، شیب مثبت به معنای روند مثبت بین داده‌های اندازه‌گیری شده است. توجه به این نکته مهم است که تفسیر مقدار به‌دست آمده برای کوواریانس ساده نیست و به زمینه موردمطالعه بستگی دارد. به عنوان مثال، مقدار کوواریانس به ما اطلاعاتی در مورد تندی شیب خط نمی‌دهد. این کمیت، تنها اطلاعاتی در مورد مثبت یا منفی بودن شیب خط به ما می‌دهد. همچنین، با دانستن مقدار کوواریانس نمی‌توانیم بگوییم آیا داده‌ها به خط رسم شده نزدیک هستند یا دور. در ادامه، فرض کنید داده‌های اندازه‌گیری شده برای ژن Y مقدارهای متفاوتی دارند. داده‌ها را با استفاده از مقدارهای اندازه‌گیری شده برای X و Y رسم می‌کنیم.

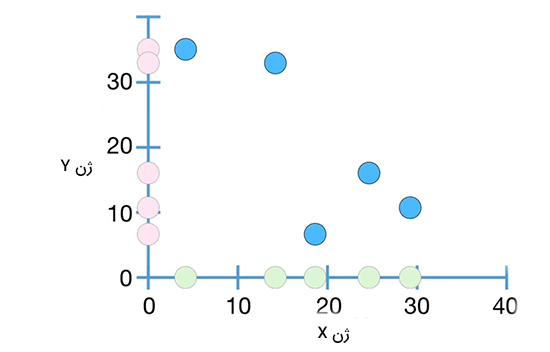
در این حالت مقدار میانگین به‌دست آمده برای داده‌های ژن X تغییر نمی‌کند، اما مقدار میانگین داده‌های ژن Y به مقدار ۲۰/۲ تغییر می‌کند. همان‌طور که در تصویر زیر دیده می‌شود، داده‌ها به دو دسته تقسیم می‌شوند:

• داده‌های بالای نمودار قرمزرنگ و سمت چپ نمودار سبزرنگ
• داده‌های پایین نمودار قرمزرنگ و سمت راست نمودار سبزرنگ

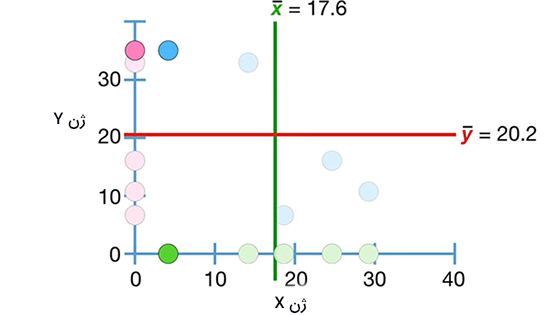
با قرار دادن داده‌ها در رابطه $$frac { sum ( x – overline { x } ) ( y – overline { y } ) } { n – 1 }$$، مقدار کوواریانس برابر ۱۰۵/۱۵- به‌دست می‌آید. از آنجا که کوواریانس به‌دست آمده منفی است، شیب خط رسم شده منفی خواهد بود.

در ادامه، کوواریانس را برای حالتی محاسبه می‌کنیم که هیچ روندی وجود ندارد.

در این حالت، مقدار داده‌های اندازه‌گیری شده برای ژن Y با یکدیگر برابر هستند. بنابراین، مقدار میانگین داده‌های این ژن، $$overline { y }$$، با مقدار هر یک از داده‌ها برابر خواهد بود. از این رو مقدار $$y – overline { y }$$ برابر صفر است. حاصل‌ضرب صفر در هر عددی نیز مقدار صفر را به ما می‌دهد. از این‌رو، مقدار کوواریانس برابر صفر به‌دست می‌آید. مقدار کوواریانس برای حالتی که داده‌های اندازه‌گیری شده برای ژن X با یکدیگر برابر هستند نیز برابر صفر خواهد بود. به این نکته توجه داشته باشید که صفر شدن مقدار کوواریانس، تنها برای داده‌های یکسان ژن X یا ژن Y برابر صفر نیست. بلکه داده‌های اندازه‌گیری شده برای هر دو ژن ممکن است به گونه‌ای تغییر کنند که باز هم مقدار کوواریانس برابر صفر به‌دست آید.

به عنوان مثال، داده‌های رسم شده در تصویر زیر به گونه‌ای تغییر می‌کنند که با افزایش داده‌های ژن X، مقدار داده‌های ژن Y افزایش و کاهش می‌یابند.

همان‌طور که در مطالب بالا اشاره شد، تفسیر مقدار به‌دست آمده برای کوواریانس سخت است. چرا؟ برای پاسخ به این پرسش، به داده‌های اندازه‌گیری شده برای ژن X برمی‌گردیم. این داده‌ها را در امتداد محورهای x و y رسم و کوواریانس آن‌ها را محاسبه می‌کنیم.

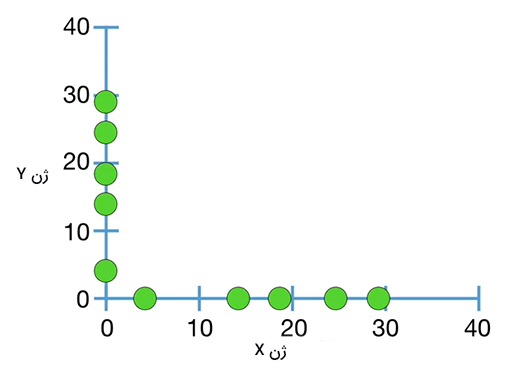
در این حالت، میانگین داده‌های در راستای محورهای x و y برابر ۱۷/۶ است.

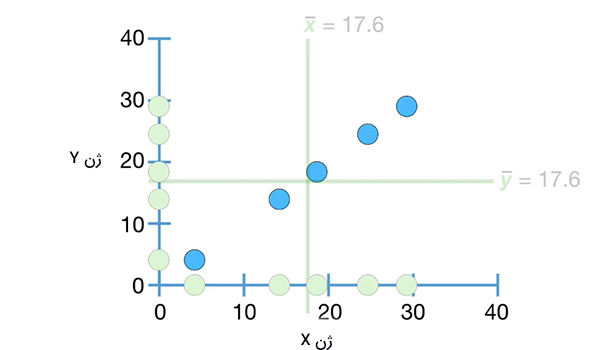
برای این حالت، رابطه $$frac { sum ( x – overline { x } ) ( y – overline { y } ) } { n – 1 }$$ را می‌توانیم به شکل زیر بنویسیم:

$$frac { sum ( x – overline { x } ) ( x – overline { x } ) } { n – 1 } = frac { sum { ( x – overline { x } )} ^ 2 } { n – 1 }$$

به بیان دیگر، کوواریانس ژن X نسبت به خودش همانند واریانس تخمین زده شده برای ژن X است. پس از انجام محاسبات، مقدار کوواریانس ۱۰۲ به‌دست می‌آید. از آنجا که مقدار به‌دست آمده مثبت است، خط تعیین‌کننده رابطه بین ژن X و خودش، شیبی مثبت خواهد داشت. اگر مقدار داده‌های ژن X را در دو ضرب کنیم، چه اتفاقی رخ می‌دهد؟ در این حالت، مقدار میانگین نیز دو برابر خواهد شد،‌ اما موقعیت نسبی داده‌ها نسبت به یکدیگر تغییر نمی‌کند. بنابراین، هر داده باز هم روی خط مستقیم مشابهی با شیب مثبت می‌افتد. به بیان دیگر، تنها موردی که تغییر می‌کند مقیاسی است که داده‌ها با آن نمایش داده می‌شوند. مقدار کوواریانس پس از دو برابر کردن داده‌ها برابر ۴۰۸ به‌دست می‌آید. این عدد، چهار برابر ۱۰۲ است.

بنابراین، مشاهده می‌کنیم که کوواریانس حتی با عدم تغییر موقعیت داده‌ها نسبت به یکدیگر، می‌تواند تغییر کند. به بیان دیگر، مقدار کوواریانس به مقیاسی که داده‌ها در آن قرار گرفته‌اند وابسته است. از این‌رو، به آسانی نمی‌توانیم آن را تحلیل کنیم. همچنین، این حساسیت سبب می‌شود که نتوانیم اطلاعاتی در مورد فاصله داده از خط روند به‌دست آوریم. اما با محاسبه کمیتی به نام همبستگی می‌توانیم اطلاعاتی در مورد فاصله داده‌ها از خط روند با شیب مثبت یا منفی به‌دست آوریم. محاسبه کوواریانس نخستین گام برای محاسبه همبستگی است.

همبستگی چیست؟

در بخش قبل با مفهوم کوواریانس آشنا شدیم. با استفاده از مقدار به‌دست آمده برای کوواریانس نمی‌توانیم اطلاعاتی در مورد فاصله داده‌ها از خط روند (خطی با شیب مثبت یا منفی)‌ به‌دست آوریم. همچنین، مقدار کوواریانس به مقیاس استفاده شده برای اندازه‌گیری وابسته است. در این بخش به اختصار با مفهوم دیگری به نام همبستگی آشنا می‌شویم. از دیدگاه آماری از همبستگی برای نشان دادن ارتباط بین دو متغیر کمی استفاده می‌کنیم. در حالت کلی این ارتباط را به صورت خطی در نظر می‌گیریم. مقدار ارتباط با کمیتی به نام ضریب همبستگی اندازه گرفته و با r نشان داده می‌شود. مقدار r می‌تواند از ۱- تا ۱- تغییر کند.

هنگامی که متغیری با افزایش متغیر دیگر، افزایش یابد، همبستگی مثبت است. اگر متغیری با افزایش متغیر دیگر، کاهش یابد، همبستگی منفی خواهد بود. اگر هیچ رابطه‌‌ای بین متغیر وجود نداشته باشد، مقدار همبستگی برابر صفر است.

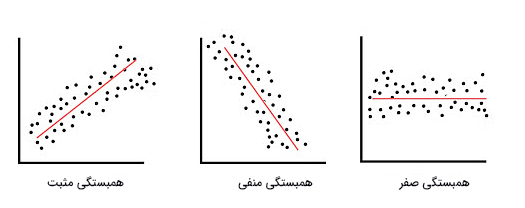
تحلیل واریانس چیست؟

فرض کنید به جای یک مجموعه داده، چند مجموعه داده داریم. سوال مهمی که ممکن است در این حالت مطرح شود آن است که چگونه می‌توانیم دو یا بیش از دو مجموعه داده را با یکدیگر مقایسه کنیم. در مباحث مرتبط با تجزیه و تحلیل آماری، گزینه‌های زیادی وجود دارند. آزمون تحلیل واریانس یکی از راه‌هایی است که به کمک آن می‌توانیم به اختلاف‌های موجود در داده‌های خود دست بیابیم. با استفاده از تحلیل واریانس در آمار می‌توانیم تفاوت بین دو گروه داده را پیدا کنیم.

با استفاده از تحلیل واریانس تفاوت بین داده‌های واقعی و برنامه‌ریزی شده را تحلیل می‌کنیم. برای انجام این کار، داده‌ها در مجموعه داده به دو گروه تقسیم می‌شوند:

• عامل‌های سیستماتیک: عامل‌هایی با تاثیر آماری بر مجموعه داده
• عامل‌های تصادفی: عامل‌هایی بدون تاثیر آماری

با استفاده از تحلیل واریانس می‌توانیم مقدار تاثیر متغیرهای مستقل بر متغیرهای وابسته را تعیین کنیم. این بررسی آماری را می‌توانیم برای بسیاری از متغیرهای مختلف در دنیای تجارت اعمال کنیم. واریانس انواع مختلفی دارد:

• واریانس کار
• واریانس فروش
• واریانس بودجه
• واریانس مواد
• واریانس سربار متغیر
• واریانس سربار ثابت

از تحلیل واریانس در کسب‌وکارهای مختلف برای ارزیابی هر انحرافی در عملکرد مالی شرکت استفاده می‌شود. همچنین، مدیرها می‌توانند بررسی بیشتری روی عملکرد عملیاتی شرکت انجام دهند و فرایندها را در محدوده بودجه شرکت نگه دارند.

بایاس و واریانس چیست؟

فرض کنید وزن و قد تعدادی موش را اندازه می‌گیریم و داده‌های به‌دست آمده را به صورت نشان داده شده در نمودار زیر رسم می‌کنیم. به طور معمول، موش‌های سبک کوتاه و موش‌های سنگین‌تر، بلندتر هستند. اما با توجه به داده‌های رسم شده در نمودار زیر، پس از رسیدن وزن موش‌ها به مقداری مشخص، قد آن‌ها افزایش نمی‌یابد. در این حالت، موش‌ها چاق‌تر می‌شوند. با استفاده از این داده‌ها می‌خواهیم، با داشتن وزن موش، قد آن را حدس بزنیم.

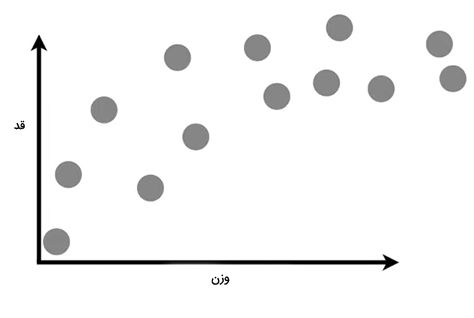
به عنوان مثال، اگر وزن موشی، مقدار نشان داده شده با علامت x روی خط افقی باشد، قدِ آن مقدار نشان داده شده با علامت ستاره روی محور عمودی خواهد بود.

در حالت ایده‌ال، فرمول دقیق ریاضی رابطه بین قد و وزن موش‌های را می‌دانیم. بنابراین، می‌توانیم با قرار دادن مقدار داده شده برای وزن در فرمول، مقدار دقیق قد موش را به‌دست آوریم. اما در اینجا این فرمول را نمی‌دانیم. بنابراین، با استفاده از دو روش یادگیری ماشین این رابطه را به صورت تقریبی به‌دست می‌آوریم. ابتدا داده‌های را به دو دسته تقسیم می‌کنیم:

• با استفاده از دسته اول به الگوریتم‌های یادگیری ماشین آموزش می‌دهیم.
• از دسته دوم برای آزمایش الگوریتم‌ها استفاده می‌کنیم.

دایره‌های آبی‌رنگ در نمودار زیر، دسته‌ای از داده‌ها هستند که برای آموزش و دایره‌های سبزرنگ دسته‌ای از داده‌ها هستند که برای آزمایش از آن‌ها استفاده می‌شود.

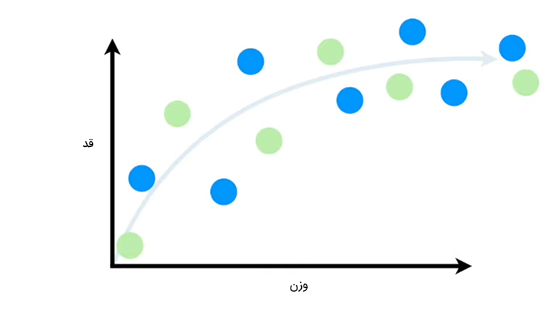
نخستین الگوریتم یادگیری ماشین که از آن استفاده می‌کنیم «رگرسیون خطی» (Linear Regression) است. با استفاده از این الگوریتم، خطی مستقیم بر داده‌های آموزشی برازش می‌کنیم. به این نکته توجه داشته باشید که خط مستقیم هرگز نمی‌تواند رابطه حقیقی بین قد و وزن موش‌ها را مشخص کند.

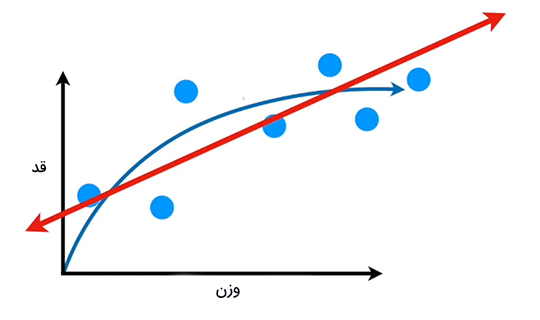
به ناتوانی روش یادگیری ماشین (مانند رگرسیون خطی)‌ در نشان دادن رابطه درست بین داده‌ها، بایاس گفته می‌شود. زیرا خط مستقیم نمی‌تواند همانند منحنی آبی‌رنگ، رابطه درست بین داده‌ها را نشان دهد. برازش خط مستقیم بر داده‌ها بایاس بسیار بزرگی دارد. در روش دیگر یادگیری ماشین می‌توانیم خط خمیده‌ای را به صورت نشان داده در تصویر زیر بر داده‌های آموزشی برازش کنیم. در این حالت، بایاس بسیار کوچک است.

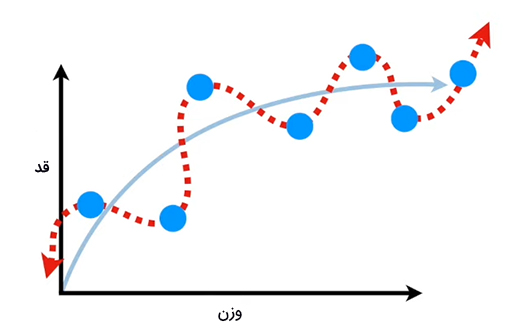
با محاسبه مجموع مربعات داده‌های آموزشی می‌توانیم برازش خط مستقیم و خط خمیده را با یکدیگر مقایسه کنیم. به بیان دیگر، فاصله هر نقطه از نمودار برازش شده را به‌دست می‌آوریم و پس از مربع فاصله‌ها، آن‌ها را با یکدیگر جمع می‌کنیم. از آنجا که فاصله‌ها به توان دو می‌رسند، فاصله‌های منفی توسط فاصله‌های مثبت خنثی نخواهند شد. در خط خمیده، فاصله بین نقطه‌ها و خط برابر صفر است. در مقایسه بین دو برازش، برازش خط خمیده پیروز می‌شود. تا اینجا به داده‌های آموزشی توجه کرده‌ایم. اما نباید از داده‌های آزمایشی غافل شویم. در ادامه، مجموع مربعات داده‌های آزمایشی را محاسبه می‌کنیم. در این حالت و در مقایسه بین دو برازش، برازش خط مستقیم پیروز خواهد شد.

بنابراین، گرچه خط خمیده به خوبی بر داده‌های آموزشی برازش می‌شود، اما برازش آن بر داده‌های آزمایشی اصلا جالب نیست. به تفاوت بین برازش‌های انجام شده بر مجموعه داده‌ها، واریانس گفته می‌شود. بایاس خط خمیده کوچک، اما تغییرپذیری یا واریانس آن بزرگ است. به بیان دیگر پیش‌بینی عملکرد خط خمیده با مجموعه داده‌ها در آینده سخت خواهد بود. در مقابل، واریانس خط مستقیم تقریبا کوچک است، زیرا مجموع مربعات برای مجموعه داده‌های مختلف بسیار مشابه یکدیگر هستند. بنابراین، خط مستقیم ممکن است در آینده پیش‌بینی‌های خوبی انجام دهد، اما این پیش‌بینی‌ها عالی نیستند.

نماد واریانس چیست؟

واریانس با نماد سیگما یا S نشان داده می‌شود. همان‌طور که در مطالب بالا فهمیدیم با استفاده از واریانس می‌توانیم میزان پراکندگی مجموعه‌ای از داده‌ها در اطراف میانگین را به‌دست آوریم. هرچه مقدار واریانس بزرگ‌تر باشد، میزان پراکندگی داده‌ها نیز بیشتر خواهد بود.

کاربرد واریانس چیست؟

همان‌طور که در مطالب بالا اشاره شد با استفاده از واریانس می‌توانیم میزان پراکندگی داده‌ها را حول میانگین بررسی کنیم. سرمایه‌گذاران با استفاده از واریانس ریسک سرمایه‌گذاری‌های مختلف و عملکرد آن‌ها را بررسی می‌کنند. همچنین، از واریانس می‌توانیم در امور مالی برای مقایسه عملکرد نسبی هر دارایی در سبد دارایی، برای دستیابی به بهترین تخصیص استفاده کنیم. به علاوه، با استفاده از واریانس می‌توان فرضیه‌های ساخته شده را آزمایش کرد. یکی از کاربردهای مهم واریانس در بازار بورس است. واریانس تاریخی هر سهم تفاوت بین بازده‌های سهم در زمان‌های متفاوت و بازده متوسط آن را اندازه می‌گیرد.

بازده سهامی با واریانس کمتر به مقدار متوسط آن نزدیک‌تر است. همچنین، بازده سهامی با واریانس بزرگ‌تر بسیار بیشتر یا کمتر از مقدار مورد انتظار خواهد بود. در این حالت، عدم قطعیت و ریسک از دست دادن سرمایه افزایش می‌یابد.

تبدیل واریانس به انحراف معیار

برای تبدیل واریانس به انحراف معیار باید از مقدار به‌دست آمده برای واریانس، جذر بگیریم.

همگنی واریانس چیست؟

همگن به معنای مشابه و ناهمگن به معنای متفاوت است. بنابراین، همگنی واریانس‌ها به معنای برابری آن‌ها است. در آمار از دو عبارت برابر و همگنی واریانس‌ها استفاده می‌شود. همان‌طور که در ابتدای بخش اشاره شد، واریانس با استفاده از فرمول زیر محاسبه می‌شود:

$$frac { sum ( x – overline { x } ) ^ 2 } { n – 1 }$$

در تصویر زیر توزیع دو مجموعه داده با واریانس یکسان و برابر ۵ را مشاهده می‌کنید. این واریانس‌ها همگن هستند.

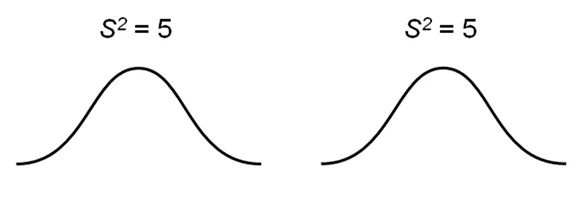
واریانس‌های ناهمگن نیز در تصویر زیر نشان داده شده‌اند. در این حالت، واریانس دو مجموعه داده با یکدیگر تفاوت دارند. همان‌طور که در تصویر زیر مشاهده می‌کنید میزان پراکندگی داده‌ها با افزایش واریانس، افزایش می‌یابد.

به عنوان مثال، دو مجموعه داده شامل تست هوش از افراد مختلف با واریانس‌های ۱۶۹ و ۲۸۹ را در نظر بگیرید که توزیع پراکندگی آن‌ها روی یکدیگر رسم شده‌اند. میانگین این دو مجموعه داده یکسان است. برای مشاهده تفاوت آن‌ها خط عمودی را به صورت نشان داده شده در تصویر زیر رسم می‌کنیم. در نمودار با واریانس کمتر، تنها ۲/۵ درصد جمعیت موردمطالعه ضریب هوشی بالاتر از ۱۳۰ و در نمودار با واریانس بزرگ‌تر، ۷/۵ درصد جمعیت مورد مطالعه ضریب هوشی بالاتر از ۱۳۰ دارند.

عامل تورم واریانس چیست؟

به اندازه‌ هم‌خطی چندگانه در تحلیل رگرسیون، «عامل تورم واریانس» (Variance Inflation Factor | VIF) گفته می‌شود. هم‌خطی چندگانه هنگامی به وجود می‌آید که بین متغیرهای مستقل مختلف در مدل رگرسیون چندگانه، همبستگی وجود داشته باشد. با استفاده از عامل تورم واریانس می‌توان میزان هم‌خطی چندگانه را بررسی کرد. عامل تورم واریانس را می‌توانیم با استفاده از فرمول زیر به‌دست آوریم:

$$VIF_i = frac { 1 } { 1 – R_ i ^ 2 }$$

در رابطه فوق، $$R_i ^ 2$$ ضریب تعیین تعدیل نشده برای رگرسیون iامین متغیر مستقل است. هرگاه $$R_i ^ 2$$ برابر صفر باشد، عامل تورم واریانس برابر یک خواهد بود. از این‌رو، iامین متغیر مستقل با مابقی متغیرها همبستگی نخواهد داشت. این بدان معنا است که هم‌خطی چندگانه وجود ندارد. در حالت کلی اگر:

• VIF برابر یک باشد، هیچ همبستگی بین متغیرها وجود ندارد.
• VIF بین یک و ۵ باشد، متغیرها نسبتا به یکدیگر همبسته هستند.
• VIF بزرگ‌تر از ۵ باشد، همبستگی بین متغیرها زیاد است.

هرچه عامل تورم واریانس بزرگ‌تر باشد، هم‌خطی چندگانه با احتمال بزرگ‌تری به وجود می‌آید. اگر عامل تورم بزرگ‌تر از ۱۰ باشد، هم‌خطی چندگانه بسیار زیاد خواهد بود. بنابراین، نیاز به پژوهش بیشتری برای اصلاح داده‌ها است.

جمع‌بندی

در این مطلب از مجله فرادرس فهمیدیم واریانس چیست. واریانس به ما میزان پراکندگی داده‌های آماری جمع‌آوری شده را نشان می‌دهد. به بیان دیگر، واریانس اطلاعاتی در مورد میزان تغییر مقدار داده‌های آماری به ما می‌دهد. هرچه مقدار واریانس بزرگ‌تر باشد، میزان پراکندگی و تغییر داده‌های آماری نیز بیشتر خواهد بود.